Is this my body? (Part II)

5 minute read

In our previous post Part I, the free-energy principle (FEP) was introduced and deployed into a humanoid robot. However, all functions and models were known. In particular, the forward model (predictor of the expected sensation given the body state) and its partial derivatives were known. How we can let the robot learn the needed functions for body perception and action? Here, we show how we can approach perceptual and active inference in the brain in a scalable machine learning point of view. For that purpose, we are going to combine variational inference with neural networks.

The model we show has been adopted from our latest work

Perception as a deep variational inference problem

Let us assume that we have a generative model able to map from our reference distribution over the latent space $q(x),$ which represents a number, encoded by the mean $\mu$ to the expected sensory input $s$ (image). We define the generative model $g$ as a nonlinear function with Gaussian noise $w_{s}:$

$s=g(\mu)+w_{s} \rightarrow s$ follows a Normal distribution $\mathcal{N}\left(g(\mu), \Sigma_{s}\right)$

We can also write the likelihood of having a sensation given our body internal variable as:

$p(s | x)=1 / \sqrt{2 \pi \Sigma_{s}} \exp \left[-\frac{1}{2 \Sigma_{s_{v}}}(s-g(\mu))^{2}\right]$

Then our variational free energy optimization under the Laplace approximation becomes:

$\dot{\mu}=-\frac{\partial F}{\partial \mu}=-\frac{\partial \ln p(s, x)}{\partial \mu}=-\frac{\partial \ln p(s | x) p(x)}{\partial \mu}$

For now, we are going to assume that the prior information about the latent space $p(x)$ is uniform and does not have any dynamics. We apply logarithms and compute the partial derivative to the likelihood $p(s | x),$ resulting in:

$\dot{\mu}=-\underbrace{\frac{\partial g(\mu)^{T}}{\partial \mu}}_{\text {mapping }} \underbrace{\Sigma_{s}^{-1}}_{\text {precision}} \underbrace{(s-g(\mu))}_{\text {prediction error }}$

In the equation above it is more clear how we compute the change on the internal variable using the error between the predicted sensation and the observed one, weighted by the relevance of that sensor. Finally, the partial derivative of the generative function gives us the mapping between the error and the latent variable.

We obtain the update rule with the first Euler integration as:

$\mu=\mu+\Delta_{t} \dot{\mu}$

For improving clarity and generalization, I will first explain the algorithm with the example of perceiving numbers with the MNIST database. We learn the decoder network that converts the latent space $\mu$ into the image of the digits 0 to 9 with the exception of number 8 that we remove from the database. After the training, we can perform the first experiment using FEP to update the belief of the world. Below you have a snippet of our PyTorch code used for computing one iteration of $\mu$ update

input = Variable(mu, requires_grad=True) # hidden variable
g = network.decoder(input) # prediction forward pass
e_v = (s - g)  # prediction error     
dF_dg = (1/Sigma_v)*self.e_v # error weighted by the precision
gv.backward(torch.ones(g.shape)*dF_dg) # backward pass
mu_dot = input.grad
mu = torch.add(self.mu, mu_dot, alpha=dt) # Update Euler integration

Experiment 1. We first initialize the latent variable to a fixed digit 0 but then the input image $s$ is 2.

The gradient descent progressively changes the latent variable producing the following shift in the predicted output $g(\mu)$

Experiment 2. The same occurs if we set $\mu$ to 7 and then we set the image of a 2 as the visual input.

The dynamics of the perception represented by its prediction is as follows:

Experiment 3. Our last test is how FEP behaves with inputs that have not been used for the training. Here we set $\mu$ to 7 and the input $s$ is 8.

The gradient optimization tries to minimize the difference between the prediction and the real observation achieving some form of five with the top part closed.

But where is the action?

In the numbers perception example, there is no action involved but one can imagine that the action will be to modify the number to better fit our initial belief.

Pixel-AI: Deep active inference

We want to scale active inference (both perception and action driven by the FEP) to visual input images with function learning. Therefore, in order to deal with raw pixels input, we developed the Pixel-AI model; a scalable model of the FEP using convolutional decoders. We deployed the algorithm in the NAO robot to evaluate its performance.

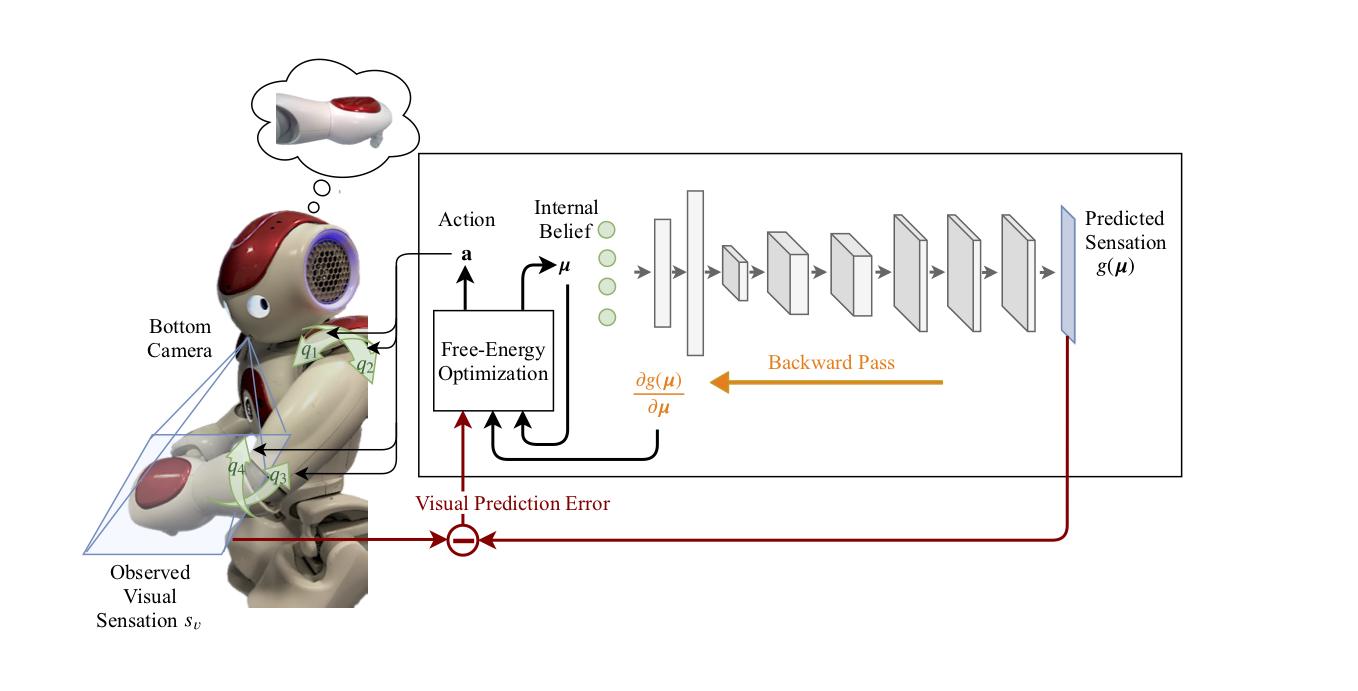
Using Pixel-Al, the robot infers its body state by minimizing the visual prediction error, i.e. the discrepancy between the camera sensor value $s_{v}$ and the expected sensation $g(\mu) .$ The internal belief of the robot corresponds to the joint angles of the robot arm. Unlike the previous model, the mapping $g(\mu)$ between the internal belief and the observed camera image is learned using a convolutional decoder. The partial derivatives $\partial g(\mu) / \partial u$ can be obtained by performing a backward pass through the convolutional decoder.

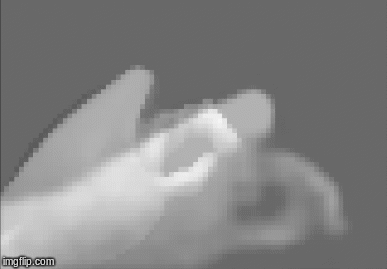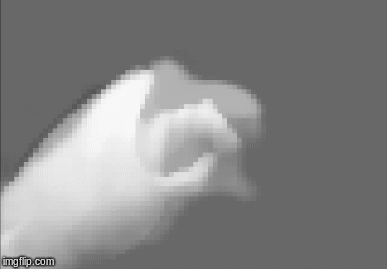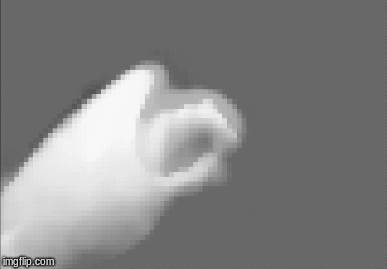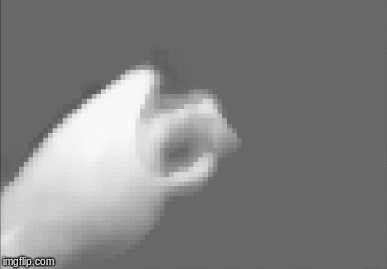
Perceptual Inference

The robot infers its body posture using the visual input provided by a monocular camera. The robot arm was brought to an initial position, but the internal belief of the body $\mu$ was set to a wrong value. As the visualizations below show, using Pixel-Al the internal belief converged to its true value so that the internally predicted visual sensation $g(\mu)$ converged to the observed visual sensation $S_{v}$. Note that here we are not using any proprioceptive information, just the raw image.

Active Inference

For the active inference tests, we used the reaching task. We set the image of a different arm configuration as an imaginary goal position. Using the actions generated by Pixel-AI, the robot’s arm converged to the goal position. The images below are with the NAO robot simulation. It is shown how the robot performs visual reaching in position and pose.

The following video shows the Pixel-AI running on the real robot. The visual goal is overlaid to the robot arm that moves until the free energy is minimized reaching the correct arm pose.

More Info

If you are interested in this research and want to learn more, check out the selfception project webpage and the related papers below. We will release the code in open source very soon. The students Guillermo Oliver and Cansu Sancaktar contributed with the research and this blog entry.

@article{sancaktar2020active,
  title={End-to-End Pixel-Based Deep Active Inference for Body Perception and Action},
  author={Sancaktar, Cansu and van Gerven, Marcel, and Lanillos, Pablo},
  journal={arXiv preprint arXiv:2001.05847},
  year={2020}
}

@inproceedings{lanillos2020robot,
  title={Robot self/other distinction: active inference meets neural networks learning in a mirror},
  author={Lanillos, Pablo and Pages, Jordi and Cheng, Gordon},
  booktitle={2020 European Conference on Artificial Intelligence (ECAI)},
  year={2020}
}

Acknowledgements. This work has been supported by SELFCEPTION project, European Union Horizon 2020 Programme under grant agreement n. 741941, the European Union’s Erasmus+ Programme, the Institute for Cognitive Systems (TUM) and the Artificial Cognitive Systems at the Donders Institute for Brain, Cognition and Behaviour.